Just for fun, imagine you could build a tower up to geosynchronous orbital height. If you stepped off the top floor, you’d just hang there, in orbit.
If the tower you build is shorter, you’d fall, since (a) you aren’t going quite as fast, and (b) orbital speed is faster as you get lower. However, you’ll be in some orbit. There should be some height, short of GEO, where the ellipse you follow doesn’t quite hit the earth. We can use the Vis viva equation and some algebra to see what that height is:
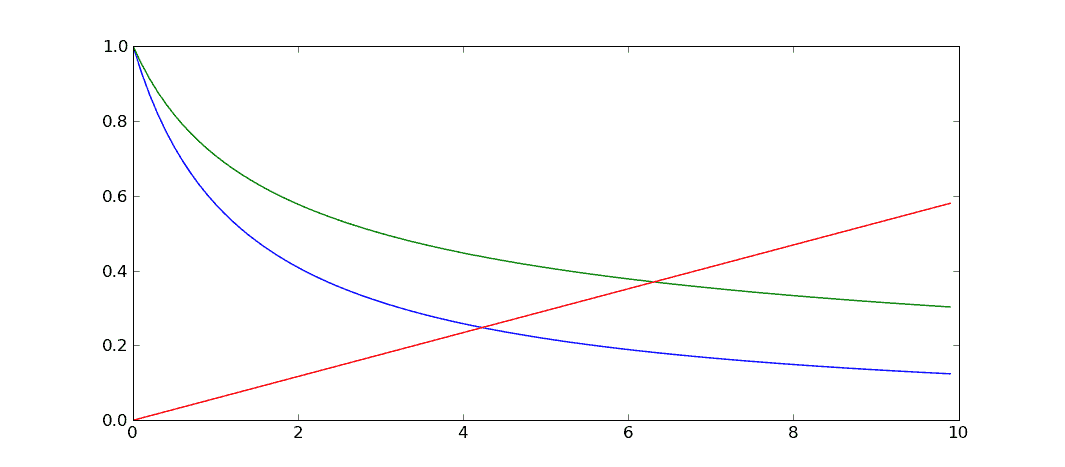
Vertical scale is kilometers per second, horizontal is kilometers height above the earth’s surface. The green line is for a circular orbit, blue for an ellipse that just misses the surface. The red line is the speed of the top of a tower of that height (at the equator).
For the blue line, elliptical orbit, you’ve saved a lot of tower height but it’s still pretty darned tall.
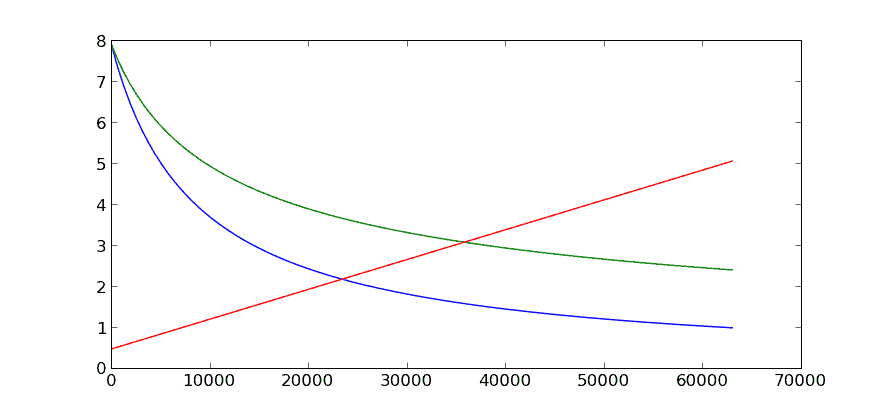
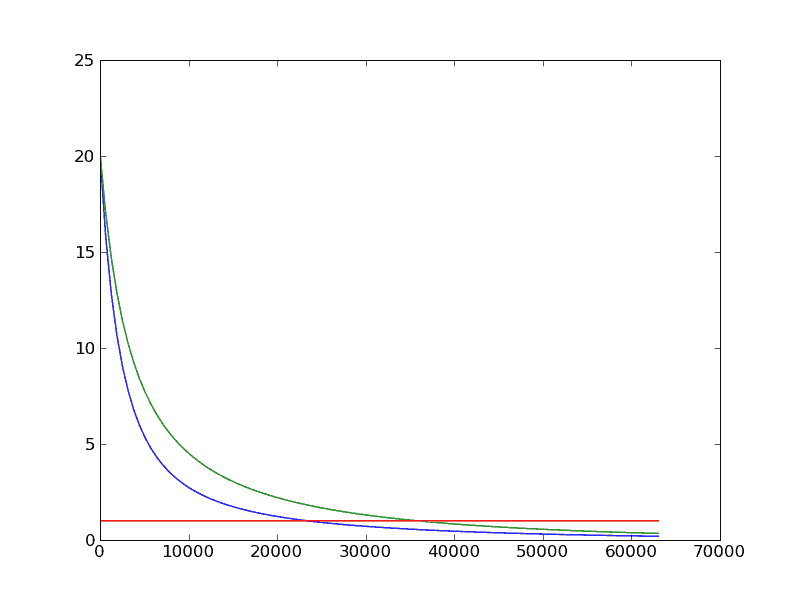
Suppose, though, you use a tower to launch rockets from. It’s well understood that you save a lot by not having to punch through the atmosphere, but you can also save a lot from the height and speed of a tower of intermediate height. The real savings shows up because of the exponential nature of the rocket equation, as we can see from the chart of the mass ratio needed in a rocket from the tower-tops:
(For a typical chemical fuel) The red line represents the part of the rocket that is the payload, and the other lines tell you how many times payload mass is the total vehicle mass. The difference is fuel you need. They cross, of course, at the same heights as stepping off works and no fuel is necessary. The knee of the curve (blue is still elliptical) is only about one earth radius (~6400km) high, a tower we could actually build with nanotech materials, where you only need about 3 payload masses of fuel to get to orbit instead of nearly 20.