Continuing our coverage of several major advances in de novo protein design recently reported by the research group of David A. Baker with a consideration of the second of the two research papers they published two months ago in Nature: “Rational design of alpha-helical tandem repeat proteins with closed architecture.” [abstract, full text PDF courtesy of the Baker lab], which concerns the rational design of a class of proteins that play important roles in binding macromolecules, as scaffolds, and as building blocks for assembling more complex materials. The University of Washington news release we cited last time continues to explain the significance of understanding and designing protein structures “Big moves in protein structure prediction and design“:
… The protein structure problem is figuring out how a protein’s chemical makeup predetermines its molecular structure, and in turn, its biological role. UW researchers have developed powerful algorithms to make unprecedented, accurate, blind predictions about the structure of large proteins of more than 200 amino acids in length. This has opened the door to predicting the structures for hundreds of thousands of recently discovered proteins in the ocean, soil, and gut microbiome.
Equally difficult is designing amino acid sequences that will fold into new protein structures.
Researchers have now shown the possibility of doing this with precision for protein folds inspired by naturally occurring proteins. More important, researchers can now devise amino acid sequences to fashion novel, previously unknown folds, far surpassing what is predicted to occur in the natural world.
The new proteins are designed with help from volunteers around the globe participating in the Rosetta@home distributed computing project. The custom-designed amino acid sequences are encoded in synthetic genes, the proteins are produced in the laboratory, and their structures are revealed through x-ray crystallography. The computer models in almost all cases match the experimentally determined crystal structures with near atomic level accuracy.
Researches have also reported new protein designs, all with near atomic level accuracy, for such shapes as barrels, sheets, rings and screws. This adds to previous achievements in designing protein cubes and spheres, and suggests the possibility of making a totally new class of protein materials.
By furthering advances such as these, researchers hope to build proteins for critical tasks in medical, environmental and industrial arenas. Examples of their goals are nanoscale tools that: boost the immune response against HIV and other recalcitrant viruses, block the flu virus so that it cannot infect cells, target drugs to cancer cells while reducing side effects, stop allergens from causing symptoms, neutralize deposits, called amyloids, thought to damage vital tissues in Alzheimer’s disease, mop up medications in the body as an antidote, and fulfill other diagnostic and therapeutic needs. Scientists are also interested in new proteins for biofuels and clean energy. …
The previous paper we reviewed here reported that a fully automated design protocol generates dozens of designs for proteins based on helix-loop-helix-loop repeat units that are very stable, have crystal structures that match the design, have very different overall shapes, and are unrelated to any natural protein. This paper presents the validation of computational methods for de novo design of protein architectures to achieve specified geometric criteria without reference to existing protein family sequences and structures.
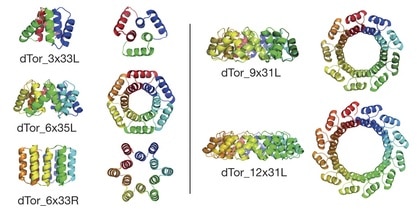
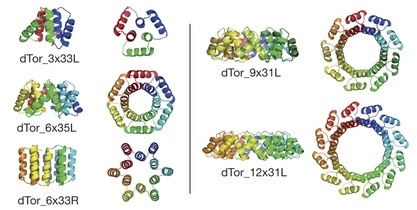
The authors note that the overall architecture of tandem repeat protein structures—dictated by the internal geometry and the local packing of the repeat building blocks—ranges from extended super-helical folds that bind RNA, RNA, or other proteins to compact, closed conformations with internal cavities suitable to binding small molecules and catalysis. They employ their computational de novo design methods to design a series of α-solenoid repeat structures, termed α-toroids, constrained to juxtapose the amino and carboxy termini of the proteins.
The closed tandem repeat architecture chosen by the authors for this paper imposes simple geometric constraints: the rise of the repeats around a central axis must be zero, and the curvature multiplied by the number of repeats must equal a multiple of 360°. Applying their design procedures produced “a diverse array of toroidal structures”. The authors explain that they focused primarily on designs with left-handed bundles because the closed, left-handed α-solenoid appeared to be absent from the structural database of known protein structures. Five families of α-toroid monomeric repeat architectures were selected for experimental characterization: a left-handed 3-repeat family, left- and right-handed 6-repeat families, a left-handed 9-repeat family, and a 12-repeat design formed by adding three repeats to one of the 9-repeat designs.
To increase the chances for successful expression, purification, and crystallization of representatives of each family, multiple designed sequences from each family were tested. Five crystal structures were determined for representatives of four of the designed toroid families. The crystal structures determined show that all four designs form left-handed α-helical toroids with the intended geometries. The deviation between the design model and experimental structure increased with the number of repeats in the design, from 0.06 nm for 3 repeats to 0.09 nm for 6 repeats, to 0.11 nm for 9 or 12 repeats. All five structures were stable to heat and to changes in protein and salt concentrations.
From these successes the authors determine that the apparent absence of this fold from the current protein structure database is not due to constraints imposed by the structure. Possibly such folds exist in natural proteins that have not yet been observed, or that region of fold space has not been sampled by natural protein evolution. Thus, the results of this research confirm the results of the paper we reviewed here last week that the known structures of natural proteins are only a small part of the structure space available to rationally designed proteins.
—James Lewis, PhD